本文为 python数据结构与算法的读书笔记,主要内容是二叉堆及用二叉堆实现优先级队列实现方式。
队列有个重要的变体,叫做优先级队列,和队列一样,优先级队列也是从头部移出元素,不过元素的逻辑顺序由优先级决定的。优先级高的元素在前面,低的在后面。因此一个元素入队时,他可能直接被移到优先级队列的头部。我们用经典的二叉堆来完成这种数据结构。
二叉堆画出来像是一棵树,但是其在python中实现只需要一个列表就可以完成,它有两个常见的变体:
- 最小堆,最小的元素一直在队首
- 最大堆,最大的元素一直在队首
二叉堆的操作
其基本操作如下:
BinaryHeap() 新建空的二叉堆insert(k) 往堆中加入一个新元素find_min() 返回最小的元素,元素留在堆中del_min() 返回最小的元素,并将该元素从堆中移除is_empty() 在堆为空时返回True,否则返回Falsesize() 返回堆中元素个数build_heap(list) 根据列表创建堆
二叉堆的实现
为了保证二叉堆对数性能,我们创建了一棵完全二叉树来维持树的平衡,从而达到要求的性能。在完全二叉树中,除了最底层,其他每一层的节点都是满的,在最底层,从左往右填充节点。如下图:
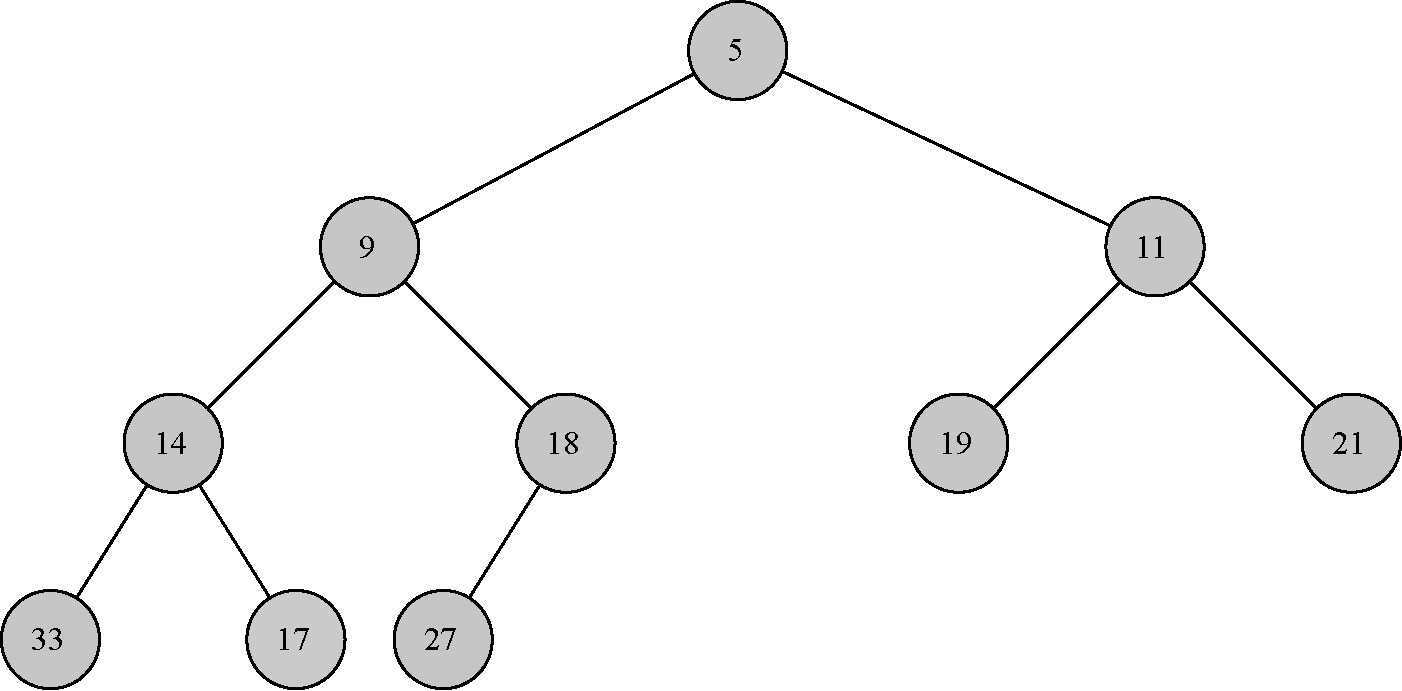
完全二叉树可以用列表来表示,而不是常用表示树的方法,如列表之列表或者节点与引用等方法表示。由于树时完全的,因此对于在列表中处于位置p的节点来说,其左子节点正好处于位置2p;右子节点处于位置2p+1。若要找到树中任意节点的父节点,只需要执行整数除法即可。
我们用来存储堆元素的方法依赖于堆的有序性,其定义为:对于堆中任意元素x及其父元素p,p都不打于x。
我们想要实现二叉堆,其主要步骤如下
- 那么首先需要是吸纳二叉堆的构造方法。首先初始化这个列表及其当前大小。
- 下一步即使实现
insert() 方法,将元素加入列表最简单高效的方式就是将元素追加到列表末尾,然后与其父节点及兄弟节点进行比较交换操作,从而维护堆的结构性质。在实现此方法之前,需要先实现向上比较交换方法perc_up() 。
- 定义完成
insert()方法之后,需要编写del_min() 方法。其查找简单,难点在于如何在移出根节点之后重新获取堆的结构性质和有序性。可以分两步完成:第一步,取出列表中最后一个元素,将其移到根节点的位置,这步操作保留了堆的性质,但破坏了二叉堆的有序性。第二步,将新的根节点沿着树推到正确的位置,以重获堆的有序性。在这步之前同样需要实现向下比较交换的方法 perc_down() 和查找最小子节点的方法min_child() 。
其代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
|
"""
@file: binary_heap.py
@author: syb
@time: 2020/06/03
"""
class BinaryHeap:
def __init__(self):
self.heap_list = [0]
self.current_size = 0
def perc_up(self, pos):
"""
向上比较并交换
:param pos:
:return:
"""
while pos // 2 > 0:
if self.heap_list[pos] < self.heap_list[pos // 2]:
self.heap_list[pos], self.heap_list[pos // 2] = self.heap_list[pos // 2], self.heap_list[pos]
pos //= 2
def perc_down(self, pos):
"""
向下比较并交换
:param pos:
:return:
"""
while pos * 2 <= self.current_size:
mc_pos = self.min_child(pos)
if self.heap_list[pos] > self.heap_list[mc_pos]:
self.heap_list[pos], self.heap_list[mc_pos] = self.heap_list[mc_pos], self.heap_list[pos]
pos = mc_pos
def min_child(self, pos):
"""
获取最小子节点位置
:param pos:
:return:
"""
if pos * 2 + 1 > self.current_size:
return pos * 2
else:
if self.heap_list[pos * 2] < self.heap_list[pos * 2 + 1]:
return pos * 2
else:
return pos * 2 + 1
def insert(self, node):
"""
插入元素
:param node:
:return:
"""
self.heap_list.append(node)
self.current_size += 1
self.perc_up(self.current_size)
def del_min(self):
"""
删除最小元素
:return:
"""
min_child = self.heap_list[1]
self.heap_list[1] = self.heap_list[self.current_size]
self.current_size -= 1
self.heap_list.pop()
self.perc_down(1)
return min_child
def is_empty(self):
"""
查看堆是否为空
:return:
"""
return False if self.current_size else True
def size(self):
"""
返回堆的大小
:return:
"""
return self.current_size
def build_heap(self, alist):
"""
从列表新建堆
"""
i = len(alist) // 2
self.current_size = len(alist)
self.heap_list = [0] + [:]
while i > 0:
self.percdown(i)
i -= 1
|

